Is 1% A Lot?

When optimizing code, is a 1% optimization (that is, an optimization that reduces run time by 1% a lot)? Well, yes and no. For any code optimization, we have to look at two important factors: leverage and repeatability.

Leverage

Let's say our game spends 90% of the time drawing the 3-d world and 10% drawing the UI. Your leverage ratios are therefore 0.9 for 3-d and 0.1 for the UI. Those are the scaling factors that discount the value of your optimizations. So a 1% optimization to the rendering engine will give you a 0.9% speed boost overall, while a 1% optimization to the UI will give you only a 0.1% speed boost overall.

So my first answer is: 1% is not a lot unless you have a lot of leverage. If your leverage ratio is 0.05 you don't have a lot of leverage, and even a 20% optimization isn't going to produce noticeable results.

This is why using an adaptive sampling profiler like Shark is so important. A Shark time profile is your code sorted by leverage. Let's take a look at a real Shark profile to see this.

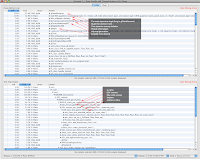
This is a Shark profile of X-Plane 9.62 on my Mac Pro in an external view with pretty much the default settings. I have used Shark's data mining features to collapse and clean the display. Basically time spent in the sub-parts of the OpenGL driver have been merged into libGL.dylib and libSys is merged to whomever calls it. We might not do this for other types of optimizations, but here we just want to see "who is expensive" and whether it's us or the GL.

The profile is "Timed Profile (All Thread States)" for just the app. This captures time spent blocking. Since X-Plane's frame-rate (which is what we want to make fast) is limited by how long it takes to go around the loop including blocking, we have to look at blocking and focus on the main thread. If we were totally CPU bound (e.g. other worker threads were using more than total available CPU resources) we might simply look at CPU use for all non-blocking threads. But that's another profile.

What do we see? In the bottoms-up view we can see our top offenders, and how much leverage we get if we can improve them. In order of maximum leverage:

1. glDrawElements! With 35.6% of thread time (that is, a leverage ratio of 0.356) the biggest single thing we could do to make X-Plane faster is to make glDrawElements execute faster. 0.356 is a huge number for an app that's already been beaten into an inch of its life with Shark for a few years.

   This isn't the first time I have Sharked X-Plane, so I can tell you a little bit of the back story. This Shark profile is on a GeForce 8800 running OS X 10.5.8; a lot of the time is OpenGL state sync in the driver (that is, the CPU preparing to send instructions to the card to change how it renders), and some is spent pushing vertex data in a less-than-efficient manner. This number is a lot smaller on 10.6 or an ATI card.

   While this call isn't in our library, we still have to ask: can we make it faster? The answer, as it turns out, is yes. When you look at what glDrawElements is doing (by removing the data mining) you'll see most of its time is spent in gldUpdateDispatch. This is the internal call to resynchronize OpenGL state. So it's really us changing OpenGL state that causes most of the time spent in glDrawElements. If we can find a way to change less state, we get a win.

2. Our quad-tree comes up next with 12.9%. That's still a big number for optimization. If we could make our quad tree faster, we might notice.

   Once again, I have looked at this issue before; in the case of the quad tree the problem is L2 cache misses - that is, the quad tree is slow because the CPU keeps waiting to get pieces of the quad tree from main memory. If we could change the allocation pattern or node structure of the quad tree to have better locality, we might get a win.

   (How do we know it's an L2 cache issue? Shark will let you profile by L2 cache misses instead of time. If a hot spot comes up with both L2 and time, it indicates that L2 misses might be the problem . If a hot spot comes up with time but not L2 misses, it means you're not missing cache, something else is making you slow.)

3. Third on the list is a real surprise - this routine tends the 3-d meshes and sees if anything needs processing. To be blunt, this stat is a surprise and almost certainly a bug, and I did a double-take when I saw it. More investigation is needed; while 7.6% isn't the biggest performance item, this is an operation that shouldn't even be on the list, so there might be a case where fixing one stupid bug gets us a nice win.

4. plot_group_layers is doing the main per-state-change drawing - it's not a huge win to optimize because the leverage isn't very high and the algorithm is already pretty optimal - that is, real work is being done here.

5. Mipmap generation is done by the driver, but we if we can use some textures without auto-mipmap generation, it might be worth it.

6. glMapBufferARB is an example of why we need to use "all thread states" - this routine can block, and when it does, we want to see why our fps is low - because our rendering thread is getting nothing done.

7. glBegin is down at 2% (leverage ratio 0.02), and this is a good example of cost-benefit trade-offs. X-Plane still has some old legacy glBegin/glEnd drawing code. That code is old and nasty and could certainly be made faster with modern batched drawing calls. But look at the leverage: 0.02. That is, if we were able to improve every single case of glBegin by a huge factor (imagine we made it 99% faster!!) we'd still see only a 2% frame-rate increase.

   Now 2% is better than not having 2%, bu it's the quantity of code that's the issue. We'd have to fix every glBegin to get that win, and the code might not even be that much faster. Because the code is so spread out and the leverage is low, we let it slide. (Over the long term glBegin code will be replaced, but we're not going to stop working on real features to fix this now.)

The profile also shows a top-down view. This view gives you a strategic view of where the overall leverage might be. We're spending 77% of our time in scenery. Right there we can say: most of the leverage is in the scenery engine - a lot more than might be in the flight model. (In fact, the entire flight model is only 5.7%.) Most of this time is then in the DSF. The airplane shows up (9.6%) but within it, the vast majority is the OBJs atttached to the airplane.

In fact, if you look at the two profiles together, the low level leverage and strategic view start to make sense . Most of that glDrawElements call is due to OBJs drawing, so it's no surprise that the airplane shows up because it has OBJs in it.

Repeatability

So the value of an optimization is only as good as its leverage, right? Well, not quite. What if one of my shaders can be optimized by 50%, but it's one of ten shaders? Well, that optimization could be worth the full 50% if I repeat the optimization on the other shaders.

In other words, if you can keep applying a trick over and over, you can start to build up real improvement even when the leverage is low. Applying an optimization to multiple code sites is a trivial example; more typically this would be a process. If I can spend a few hours and get a 1% improvement in shader code, that's not huge. But if I can do that every day for a week, that might turn into a 10% win.

So to answer the question "is 1% a lot", the answer is: yes if the leverage is there and you're going to keep beating on the code over and over.

Basis Projection

In my previous post I described a transform matrix as a sort of kit of "premade parts" that each vertex's components call out. Thus a vertex of (1, 0.5, 0) means "use 1 measure of the X basis from the matrix, 0.5 measures of the Y basis, and skip the Z basis, we don't want any of that." You can almost see a matrix as a form of encoding or compression, where we decode using the "premade parts" that are basis vectors. (I must admit, this is not a very good form of compression, as we don't save any memory.)

So if our model's vertices are encoded (into "model space") and a model positioning matrix decodes our model into world space (so we can show our model in lots of places in the world), how do we encode that model? If we have one house in world space, how do we encode it into its own model space?

One way to do so would be "basis projection". We could take the dot product of each vector in our model* with each basis vector, and that ratio of correlation would tell us how much of the encoding vector we want. What would a matrix for this encoding look like?

[x][Xx Xy Xz]
[y][Yx Yy Yz]
[z][Zx Zy Zz]

where we are encoding into the vector X, Y, and Z, described in the world coordinates.

So we have put our basis vectors for our model into the rows of the matrix to encode, while last time we put them into the columns to decode.

Wait - this isn't surprising. The encode and decode matrices are inverses and the inverse of an orthogonal matrix is its transpose.

Putting this together, we can say that our orthogonal matrix has the old basis in the new coordinate system in its columns at the same time as it has the new basis in the old coordinate system in its rows. We can view our matrix through either the lens of decoding (via columns - each column is a "premade part") or encoding (via rows - how closely do we fit that "premade part").

Why bring this up? The previous post was meant to serve two purposes:

1. To justify some particularly sparse implementations of camera operations. (E.g. how did we get the code down to so few operations, why is this legal?)
2. To try to illustrate the connection between the symbols and geometric meaning of matrices and vectors.

The observation that basis projection and application are two sides of the same coin is a segue into my next post, which will be on the core foundation of spherical harmonics, which is basically the same basis trick, except this time we are going to get compression - a lot of it.

* As in the previous article, we can think of our model as a series of vectors from the origin to the vertices in our mesh.

Change of Basis, Revisited

A while ago I suggested that we could find the billboard vectors (that is, the vectors aligned with the screen in model-view space) simply by looking at the matrix itself. A commenter further pointed out that we could simply transpose the upper 3x3 of our model-view matrix to invert the rotational component of our matrix. Let's look at these ideas again.

Transform Matrix As Basis Vectors

If we have a 3x3 matrix T of the form:

[a d g]
[b e h]
[c f i]

Then when we multiply a vector (x,y,z) by this matrix T, x gives us more or less of (a,b,c), y of (d,e,f) and z of (g,h,i). In other words, you can think of x, y, and z being orders for premade "amounts" of 3 vectors. In the old coordinate system, x gave us one unit of the 'x' axis, y one unit of the 'y' axis, and z one unit of the 'z' axis. So we can see (a,b,c) as the old coordinate system's "x" axis expressed in the new coordinate system, etc.

This "change of basis" is essentially an arbitrary rotation about the origin - we are taking our model and changing where its axes are. Use the data with the old axes and you have the model rotated. So far everything we have done is with vectors, but you can think of a point cloud as a series of vectors from the origin to the data points.

Big Words

A lot of math for computer programmers is just learning what the mathematicians are talking about - math has a lot of vocabulary to describe ideas. Sometimes the words are harder than the ideas.

Our rotation matrix above is a set of orthonormal basis vectors. (We call the matrix an orthogonal matrix.) What does that mean? It means two things:

• Each basis vector is normal - that is, its length is 1.
• Each basis vector is orthogonal to all other basis vectors - that is, any two basis vectors are at right angles to each other.

We'll come back to these mathematical properties later, but for now, let's consider what this means for our view of a transform matrix as using "premade pieces" of the coordinate axes.

• Our model isn't going to change size, because each basis vector is of length 1 (and in the original coordinate system, 1 unit is 1 unit by definition).
• Because the axes are all orthogonal to each other, we're not going to get any squishing or dimension loss - a cube will stay cubic. (This would not be true if we had a projection matrix! Everything we say here is based on fairly limited use of the model-view matrix and will not be even remotely true for a projection matrix.)
  

Translation Too

If we want to reposition our model completely (rotate and translate) we need a translation component. In OpenGL we do that like this:

[ x]
[ R y]
[ z]
[0 0 0 1]

In this matrix, R is our 3x3 rotation matrix, which is orthogonal, x y z is the offset to apply to all points. If we apply this to vectors of the form (x,y,z,1) then the math works out to first rotate the points x,y,z by r, and then add x,y,z after rotation. The last coordinate 'w' will remain "1" for future use. The upper right 3x3 matrix is orthogonal, but the whole matrix is not; if this were a 4-dimensional basis change, the vector (x,y,z,1) would not necessarily be normalized, nor would it be perpendicular to all other bases.

There's a name for this too: an affine transformation matrix. If we ever have a liner transform (of which a set of orthonormal basis vectors is one) plus a translation, with 0....1 on the bottom, we have an affine transformation.

Affine Transformation As Model Position

If we have an affine transform matrix built from three orthonormal basis vectors (our old axes in the new coordinate system) plus an offset, we have everything we need to position a model in 3-d space. Imagine we have a house model, authored as points located around an origin. We want to position it at many locations in our 3-d world and draw it each time. We can build the transform matrix we want. Typically we'd do a sequence like:

glTranslate(x,y,z);
glRotate(heading,0,1,0);
glRotate(pitch,1,0,0);
glRotate(roll,0,0,1);

That is, first move the models origin to this place in world space, then rotate it. This forms an affine matrix where the right most column is x,y,z,1 and the left three columns are the location of the model's X, Y, and Z axes in world space (with 0 in the last digit). The bottom row is 0 0 0 1.

Usually it's cheaper storage-wise to store the component parts of a model's transform than the entire transform matrix. But if we do want to store the object in the format of a transform, we do know a few things:

• The bottom row is 0 0 0 1 so we can simply delete it, cutting our matrix down from 16 floats to 12.
• We can get the object "location" in world-space directly out of the right-hand column.
• The upper-left 3x3 matrix contains all of the rotations.

If we have only used rotations and not mirroring, we can decode the Euler angles of the rotation from this upper left 3x3; that'll have to be another post.

The main reason to store model location as a matrix (and not the original offset and rotation angles) is for hardware instancing; we can stream a buffer of 12-float matrices to the GPU and ask it to iterate over the mesh using something like GL_ARB_draw_instanced. But if you're on an embedded platform and stuck in fixed point, replacing angles (which require trig to decode) with the matrix might also be a win.

glScale Wasn't Invited To The Party

We cannot scale our model using glScale and still have an orthonormal basis; doing so with any scale values other than 1 or -1 would make the basis vectors be non-unit-length, and then it would not be orthonormal. We can have mirroring operations - there is no requirement that an orthonormal basis maintain the "right-handedness" of a coordinate system.

With X-Plane we don' do either of these things (scale or mirror); in the first case, we don't need it, and it's a big win to know that your upper left 3x3 is orthonormal - it means you can use it to transform normal vectors directly. (If the upper left 3x3 of your model-view scales uniformly, your normals change length, which must be fixed in shader. If your model-view scales non-uniformly, the direction of your normals get skewed.) We don't mirror because there's no need for it, and for a rendering system like OpenGL that uses triangle direction to back-face-cull, changing the coordinate system from right-handed to left-handed would require changing back-face culling to match.

Stupid Matrix Tricks

There are a few nice mathematical properties of orthogonal matrices. First, the transpose of the matrix is its inverse. To demonstrate this, take an orthogonal matrix and multiply it by its transpose. You'll find that every component is either the dot product of two orthogonal vectors or a unit length vector with itself, thus it forms the 0s and 1s of an identity matrix.

That's cool right there - it means we can use a fast operation (transpose) instead of a slow operation (invert) on our upper left 3x3. It also means that the inverse of an orthogonal matrix is orthogonal too. (Since the inverse is the transpose, you can first invert your matrix by transposing, then multiply that new matrix by its transpose, which is the original, and multiply the components out - you'll find the same identity pattern again.)

If an orthogonal matrix's inverse is orthogonal, so is its transpose, and from that you can show that multiplying two orthogonal matrices forms a new orthogonal matrix - that is, batching up orthogonal matrix transforms preserves the orthognality. (You can calculate the components of the two matrices, and calculate the transpose from the multiplication of the transposes of the sources in opposite order. When you manipulate the algebra, you can show that the multiplication of the two orthogonal matrices has its transpose as its inverse too.)

If we know that an orthogonal matrix stays orthogonal when we multiply them, we can also show that affine matrices stay affine when we multiply them. (To do this, apply an affine matrix to another affine matrix and note that the orthogonal upper left 3x3 is only affected by the other matrices' upper 3x3, and the bottom row stays 0 0 0 1.) That's handy because it means that we can pre-multiply a pile of affine transform matrices and still know that it's affine, and that all of our tricks apply.

Camera Transforms

Camera transforms are funny beasts: when we move the camera, we do the opposite transforms of moving the model, and we do them in the opposite order. So while we positioned our model by first translating, then rotating, we position our camera by first rotating, then translating, and we do everything in the opposite order. (Consider if we want to position the camera at 10,0,0 in world space, we really achieve this by moving the model to -10,0,0.)

This means we can't recover information about our camera location directly from the modelview matrix. But thanks to all of the properties above, we can make camera angle recovery cheap.

Our orthogonal matrix contains the location of the old coordinate system's axes (in terms of the new coordinate system) as columns. But since its transpose is its inverse, it also contains the location of the new coordinate sytem's axes (in terms of the old coordinate system) as rows. Our model view matrix transforms from world space to camera space. So we have the axes of the camera space (that is, the "X" axis of camera space/eye space is an axis going to the right on your monitor) in terms of world space, right there in the rows. Thus we can use the first, second and third row of the upper left 3x3 of an affine transform matrix to know the billboard vectors of an affine modelview matrix.

The location of the camera is slightly trickier. The right most column isn't the negative of the position of the camera. Why not? Well, remember our "model positioning" transform was a translate-then-rotate matrix, with the translation in the right column. But camera transforms happen in the opposite order (negative-, then negative-translate). So the location of the camera is already "pre-rotated". Doh.

Fortunately we have the inverse of the rotation - it's just the transpose of the orthogonal 3x3 upper left of our affine matrix. So to restore the camera location from a model-view matrix we just need to multiply the upper right 1x3 column (the translation) by the transpose of the upper left 3x3 (the rotation) and then negate.

Having the camera direction and location in terms of the modelview matrix is handy when we have code that applies a pile of nested transforms. If we have gone from world to aircraft to engine coordinates (and the engine might be canted), we're in pretty deep. What are the billboarding vectors? How far from the engine are we? Fortunately we can get them right off of the modelview matrix.

EDIT: one quick note: an affine transform is still affine even if the upper left matrix isn't orthogonal; it only needs to be linear. But if we do have an orthogonal matrix in the upper left of our affine matrix, multiplying two of these "affine-orthogonal" matrices together does preserve both the affine-ness of the whole matrix and the orthogonality of the upper left. I'm not sure if there is an official name for an affine matrix with an orthogonal upper left.

More STL Abstraction

A while ago I made the claim that the STL is not an abstraction because the specification it implements is so specific with regard to performance that it's really just an implementation. Response was swift and furious, and my contrast of the STL to something like an SQL query may have been lost.

Which begs the question: why is anyone reading this? What the heck? Chris and I have been terrified to find anything from this blog on the first page of a Google search or reposted somewhere. So if you're reading this: there will be no refunds at the end of this article if you feel you've lost 5 minutes of your life you'll never get back. You have been warned.

Anyway, I was looking at one case of the STL where you actually don't know what kind of performance you'll get unless you know things about your specific implementation. When you insert a range into a vector, the insert code has two choices:

1. Iterate the range once, incrementally inserting. This may cause excess reallocation (since we don't know how much more memory we need until we're done), and that reallocation may in turn call excess copy construction and destruction.
2. Measure the distance of the range. This lets us do one allocation and a minimum number of copies, but if the iterator doesn't have random access differencing, it would mean the range is iterated twice.

The GCC 4 STL that we use will only pick choice 2 if the iterator is known to be random access. (I haven't scrubbed the traits system to see how good it is at determining this when iterators don't use appropriate tags.) Whether this is a win or not can't be known by the STL, as it doesn't know the relative cost of iteration vs. object copy vs. memory allocation.

I have seen other cases where you can't quite guess what STL performance might be. For example, some implementations cache list size for O(1) list::size() while others do not cache and have to actually traverse the list. The SGI STL documentation does declare what the worst behavior is, so I have no right to complain if the list size isn't cached.

My argument isn't that the STL should always do the right thing by reading my mind. My argument is that because the STL is such a low level of abstraction, and because it serves such a low level purpose in code, the performance of the implementation matters. There may not be one right container for the job, and in trying to decide between a vector and list, whether I get single-allocate-insert on vector or constant-time size on the list might matter.

Fortunately in real development this turns out to be moot; if performance matters, we'll run an adaptive sampling profiler like Shark on the app, which will tell us whether for our particular usage and data the STL is under-performing. In a number of cases, our solution has been to toss out the STL entirely for something more efficient; as long as that's on the table we're going to have to profile, which will catch STL implementation differences too.

The Value Of Gamma Compression

A number of engineers all had the same response to the sRGB/Gamma thread on the Mac OpenGL list: life would be a lot easier if color were linear. Yes, it would be easier. But would it be beautiful?

The answer is: not at 8 bits, and definitely not with DXT compression.

The following images show a gray-scale bar, quantized to: 16, 8, 6, and 5 bits per channel. (16-bits per channel would be typical of a floating point, HDR, or art asset pipeline, 8-bits is what most apps will have to run on the GPU, and 5/6 bits simulate the banding in the key colors of DXT-compressed textures, which are 5-6-5.)





In the images labeled "srgb" (gamma is 1.0) the colors are quantized in sRGB (non-linear) space. Becuase sRGB is perceptually even, the banding appears to be even to a human - it's a good use of our limits bits. 8-bit color is pretty much smooth, and artifacts are minimized for 5 and 6 bits (although we can definitely see some banding here.)

Now what happens if we quantize in linear space? You'd get this:





Note: the program generates these ramps in sRGB space (hence they are "evenly spaced", converts to linear, quantizes, then converts back. So this is what your textures would look like if your art assets were converted to and stored linearly.

What can we see? Well, if we have 16-bits per channel we're still okay. But at 8-bits (the normal way to send an uncompressed texture to the GPU) we have visible banding in the darker regions. This is because linear isn't an efficient way to space out limited bits for our eyes.

The situation is really bad for the 6 and 5-bit compressed textures; we have so little bandwidth that the entire dark side of the spectrum is horribly quantized.

The moral of the story (if there is one): gamma is your friend - it's non-linear, which is annoying for lighting shaders, but when you have 8 bits or less, it puts the bits where you need them.

I hate C, part 492.

FMTT.

HIWindowCopyColorSpace_f = (CGColorSpaceRef (*)(WindowRef))

CFBundleGetFunctionPointerForName, tib, CFSTR("_HIWindowCopyColorSpace");

HIWindowSetColorSpace_f = (OSStatus (*)(WindowRef,CGColorSpaceRef))

CFBundleGetFunctionPointerForName, tib, CFSTR("_HIWindowSetColorSpace");

The set of legal C programs is just not that different from the set of ASCII strings.

Gamma and Lighting Part 3: Errata

A few other random notes for working with lighting in linear space...

Light Accumulation

In order to get correct lighting, lights need to be accumulated (that is, the contribution of each light to any given pixel) in linear space. There are three ways to do this safely:

1. Accumulate all lights in a single pass. The sum happens in your shader (which must calculate each light's contribution and add them). This is typical of a traditional one-pass forward renderer, and is straight forward to convert to linear space. The lighting calculation is done linearly in shader, converted to something with gamma, then written to an 8-bit framebuffer.

   Clamping and exposure control are up to you and can happen in-shader while you are in floating point.

2. Multi-pass with sRGB_framebuffer. If you want to accumulate lights by blending (e.g. using blending to add more "light" into the framebuffer and your framebuffer is 24-bit RGB, you'll need the sRGB_framebuffer extension. This will cause OpenGL to not only accept linear fragments from you, but the blending addition will happen in linear space too.

   In this case, exposure control is tricky; you don't want to saturate your framebuffer, but no one lighting pass knows the total exposure. You'll have to set your exposure so that the conversion to sRGB doesn't "clip".

3. Multi-pass with an HDR framebuffer. The other option for accumulating light by blending is to use a floating point framebuffer. This configuration (like mutli-pass with sRGB) might be typical of a deferred renderer (or a stencil-shadow-volume solution).

   Unlike sRGB into a 24-bit framebuffer, this case doesn't have a clipping problem, because you can write linear vlaues into the floating point framebuffer. You do need to "mix down" the floating point framebuffer back to sRGB later.

What you cannot do is convert back to sRGB in your shader and then use regular blending. Doing so will add lights in sRGB space, which is incorrect and will lead to blown out or clipped lights wherever they overlap.

What Color Space Is The Mac Framebuffer?

On OS X 10.5 and older, your framebuffer will have the color profile of the device, at least as far as I can tell. This probably means that the effective gamma is 1.8 (since the OS's color management should adjust the LUT enough to achieve this net result).

On OS X 10.6 every window has its own color profile, and the window manager color-converts as needed to get correct output on multiple devices. Edit: By default you get the monitor's default color profile, but you can use HIWindowSetColorSpace to change what color profile you work in.

Gamma and Lighting Part 2: Working in Linear Space

In my previous post I tried to describe the process of maintaining color sync. Two important things to note:

• Most color spaces that are reasonable for 24-bit framebuffers aren't linear. Twice the RGB means a lot more than twice the luminance.
  
• This is good from a data-size standpoint, because 8 bits for channel isn't enough to be linear.

But there's a problem: this non-linear encoding is not good if we're going to perform 3-d calculations to create computer-generated images of light sources. Note that this is not an issue of monitor calibration or which gamma curve (Mac or PC) you use; no color space with any gamma is going to be even remotely close to linear luminance. So this is almost a 'wrong format' issue and not a 'wrong calibration' issue.

Consider: light is additive - if we add more photons, we get more light. This is at the heart of a computer graphics lighting model, where we sum the contribution of several lights to come up with a luminance for an RGB pixel. But remember the math from the previous post: doubling the RGB value more than doubles the luminance from your monitor.

In order to correctly create lighting effects, we need to:

1. Convert from sRGB to linear color.
2. Do the lighting accumulation in linear color space.
3. Convert back to sRGB because that's the format the framebuffer needs.

Doing this makes a huge difference in the quality of lighting. When physical lighting calculations are done directly in sRGB space, intermediate light levels are too dark (cutting the sRGB value in half cuts the luminance by a factor of five!) and additive effects become super-bright in their center. I found that I can also set ambient lighting to be lower when using correct linear lighting because the intermediate colors aren't so dark. (With intermediate colors dark, you have to turn up ambience or the whole image will be dark.)

Let the GPU Do It

The OpenGL extensions GL_EXT_texure_sRGB and GL_ARB_framebuffer_sRGB basically do steps 1 and 3 for you; when you set a texture's internal type to sRGB, the GPU converts from sRGB to linear space during texel fetch. When framebuffer_sRGB is enabled, the GPU converts from linear back to sRGB before writing your fragment out to the framebuffer. Thus your shader runs in linear space (which is fine because it has floating point precision) while your textures and framebuffer are sRGB like they've always been.*

The advantage of using these extensions on DirectX 10 hardware is that the conversion happens before texture filtering and after framebuffer blending - two operations you couldn't "fix" manually in your shader. So you get linear blending too, which makes the blend of colors look correct.

Of course, your internal art asset format has to be sRGB in order for this to work, because it's the only color space the GL will convert from and back to.

* The question of whether your framebuffer is sRGB or linear is really more a question of naming convention. If you go back 10 years, you know a few things: writing RGB values into the framebuffer probably produces color on the monitor that is close to what you'd expect from sRGB, but the GL does all lighting math linearly. So it's really sRGB data being pushed through a linear pipeline, which is wrong and the source of lighting artifacts.

Gamma and Lighting Part 1: Color Sync

The topic of color spaces, gamma, and color correction gets complex and muddled quickly enough that I had to delete my post and start over. Fortunately a number of folks on the Mac OpenGL list set me straight. This first post will discuss how to control color when working with textures; the second one will address how to light those textures in 3-d.

This FAQ explains Gamma infinitely better than I possibly can. I suggest reading it about eight times.

24-bit Color Spaces Are Pretty Much Never Linear

A color space defines the meaning of RGB colors (that is, triplets of 8-bit or more codes). How red is red? That's what your color space tells you. And the first thing I must point out is: no color space you'd ever use on an 8-bit-per-channel (24-bit color) display is ever going to have a linear mapping between RGB values and luminance. Why not? This Wikipedia article on sRGB puts it best:

This nonlinear conversion means that sRGB is a reasonably efficient use of the values in an integer-based image file to display human-discernible light levels.

Here's what's going on:

• Our perception of color is non-linear. It's roughly logarithmic. This means we're more discerning of light level changes at low light levels. That's good - we can see in the dark, sort of, or at least this improves our dynamic range of light perception.
• 256 levels of gray isn't a lot, so it's important that the levels be spread out evenly in terms of what humans perceive. Otherwise we'd run out of distinct gray levels and see banding.
• Therefore, to make 24-bit images look good, pretty much every color space including sRGB is radically different from linear luminance levels.

When we discuss images with different gamma below, let's just keep this in the back of our mind: pretty much any sane color space is going to have some gamma if it will be used for 24-bit images, and that's good because it lets us avoid banding and other artifacts. It will also become important when we get to lighting.

Part of the confusion over gamma correction is that CRTs have non-linear response by nature of their electronics. People assume that this is bad and that gamma correction curves make the RGB->luminance response linear. In fact, that response is actually useful, and that's why the gamma correction curves on a computer typically undo some of the non-linear response. For example, Macs used to bring the gamma curve down to 1.8 (from 2.5 for a CRT) but not all the way down to 1.0. As mentioned above, if we really had linear response between our RGB colors and luminance, we would need more than 8 bits per channel.

Consistent Color

If we are going to develop a simulator that renders using OpenGL onto a PC or Mac, we're going to work in a color space, probably with 24-bit color most of the time. (We might use higher bit depths in advanced rendering modes, but we can't afford to store our entire texture set in a higher res. Heck, it's expensive to even turn off texture compression!)

So the important thing is that color is maintained consistently through the authoring pipeline to the end user. In practice that means:

1. Artists need to have their monitors correctly calibrated. If the artist's monitor isn't showing enough red, the artist paints everything to be too red, and the final results look Mars-tacular. So the artist needs good "monitoring."

2. The color space needs to be tracked through the entire production process. Whether this happens by simply declaring a global color space for the entire pipeline or by tagging assets, we need to make sure that red keeps meaning the same red, or that if we change it, we record that we've changed it and correctly adjust the image.

   When working with PNG, we try to record the gamma curve on the PNG file. We encourage our artists to work entirely in sRGB.

3. The graphics engine needs to not trash the color on read-in. Similar to the pipeline, we need to either not mess up the colors, or track any change in color space. In X-Plane's space, X-Plane will try to run in approximately the color space of the end user's machine, so X-Plane's texture loader will change the color space of textures at load time.

4. The graphics engine needs to cope with a user whose display is atypical (or not). Finally, if the user's display is not in the same color space as the production pipeline, the engine needs to adjust its output. (Or not adjust its output and expect the user to fix it locally.) In X-plane's case we do this by using the user's machine's gamma curve and correcting images at load time.

   This is not the best solution for color accuracy; it would be better to keep the images in their saved color space and convert color in-shader (where we have floating point instead of 8-bits per channel). Historically X-Plane does the cheap conversion to save fill rate. We may some day change this.

(Note: pre-converting color is particularly a poor idea for DXT-compressed textures, because you can adjust the pair of 565 key colors in each block but you can't adjust the weightings, which are clamped at fixed mix-points based on the DXT specification. So the mid-tone colors for each block will be distorted by trying to color correct a compressed image.)

If all of these steps are taken, the end user should see textures just as the art team authored them. Before we had step four in X-Plane, PC users used to report that X-Plane was "too dark" because their monitor's color response wasn't the same as our art team's (who were using Macs). Now they report that X-Plane is too dark because it's dark. :-)

In my next post I'll discuss the relationship between non-linear color spaces (that work well in 24-bit color) and 3-d lighting models.

The Very Best Seventies Technology

I do not like Lisp. Actually, that's not quite correct. I despite Lisp the way Red Sox fans despise the Yankees and Glenn Beck despises fiat money. (BTW there has never been a better time to buy gold. Srsly.) Lisp is not a computer language; it is a cult that warps the minds of otherwise capable programmers and twists their very notion of what a program is.*

So it is in this context that I began a conscious campaign to reduce the number of parenthesis in my C++. I know, some of you may be saying "say what you mean, understand what you say" and all of that feel-good mumbo jumbo. Heck, my own brother told me not to minimize parens. But I can't have my carefully crafted C++ looking like Lisp. It just won't do.

So slowly I started to pay attention to operator precedence, to see when I didn't actually need all of those "safety" parens. And here's what I found: 95% of the time, the C operator precedence makes the easy and obvious expression the default. I was actually surprised by this, because on the face of it the order looks pretty arbitrary.

If you squint though, you'll see a few useful groups:

• Unary operators before binary operators.
• Math before comparison.
• Comparison before anything if-like (e.g. && which is more like control flow than an operator).
• Assignment at the bottom.

There's just one rub: comparison is higher precedence than bit-wise binary operators, which is to say:

if( value & mask == flag)

doesn't do what you want. You have to write the more annoying:

if((value & mask) == flag)

So what went wrong? It turns out there's a reason!

Approximately 5,318 years ago when compilers were made out of yarn and a byte only had five bits, C was being built within the context of B and BCPL. If you thought C was cryptic and obtuse, you should see B and BCPL. B is like C if you removed anything that might tell you what the hell is actually going on, and BCPL looks like you took C, put it in a blender with about 3 or 4 other languages, and played "will it blend". (Since BCPL is "no longer in common use", apparently the answer is no. But I guess they couldn't have thought it looked like a C blend at the time, as C hadn't been invented.)

Anyway, in B and BCPL, & and | had a sort of magic property: inside an if statement they used lazy evaluation (like && and || in C/C++) - they wouldn't even bother with the second operand if the first was true or false. So you could write things like this: if(ptr & ptr->value) safely. But you could also write flag = ptr & 1; to extract the low bit.

In a rare moment of preferring sanity over voodoo, Dennis Ritchie chose to split & and | into two operators: | and & would be bit-wise and always evaluate both operators, while && and || would work logically and short-circuit. But since they already had piles of code using & as both, they had to keep the precedence of & the same as in B/BCPL (that is, low precedence like &&) or go back and add parens to all existing code.

So while & could be higher precedence, it's not for historical reasons. But have patience; we've only had to live with this for 38 years. I am sure that in another 40 or 50 years we'll clean things up a bit.

* A program is a huge mess of confusing punctuation. Something clean and elegant like this: for(;P("\n"),R=;P("|"))for(e=C;e=P("_"+(*u++/ 8)%2))P("|"+(*u/4)%2);

Finding Mom and Dad

I was looking to use generic programming to clean up some otherwise picky code today, but I fear I can't find a way to do it that doesn't cost me storage. (Well, that's not 100% true, but I digress.)

There may be cases where I have an object O with sub-parts S1, S2, etc. where the implementation of S1/S2 could be made more efficient if part of their data could be pushed out to O. An example would be an object containing several intrinsic linked lists. The linked lists can be made faster by maintaining a stack of unused nodes, like this:

struct node {
node * next;
...
};
struct O {
node * S1_list_head;
node * S2_list_head;
node * free_stack_top;
};

Our object contains two lists, but only one common stack pool.

We can use templates to safely hide away the maintenance of this code, sort of, e.g.

template
void pop_front(node *& head_list, node *& free_list)
{
* k = head_list;
head_list = head_list->next;
k->next = free_list;
free_list = k;
}

There's just one problem: if we call pop_front and reverse the argument order for our head and free list, we are going to create a world of hurt. What we really want is something like S1_head_list.pop_front();

What I can't seem to find is a way to turn S1 and S2 into objects that have knowledge of their contained parts. In the above case, we would have to template S1 and S2 based on their byte offset from themselves to the location of their common section in the parent. That's something the compiler knows, but won't tell us, and we don't want to figure out by hand.

The best real alternative I suppose would be to wrap the templated list function in something inside O and then make the lists private, limiting the number of cases where a usage error of the template functions can occur.

The traditional work-around for this would be to include a pointer to O inside S1 and S2. This is clean and fool-proof, but also increases the storage requirements of S1 and S2; if we are storage sensitive to O, this isn't acceptable.

MediaWiki and ModSecurity

We were seeing 500 Internal Server Errors:

The server encountered an internal error or misconfiguration and was unable to complete your request.
Please contact the server administrator, webmaster@xsquawkbox.net and inform them of the time the error occurred, and anything you might have done that may have caused the error.
More information about this error may be available in the server error log.

My host finally figured out what was going wrong. This was in /www/logs/error_log:

Wed Nov 10 12:48:15 2010] [error] [client 71.248.161.106] ModSecurity: Access denied with code 500 (phase 2). Pattern match "(insert[[:space:]]+into.+values|select.*from.+[a-z|A-Z|0-9]|select.+from|bulk[[:space:]]+insert|union.+select|convert.+\\(.*from)" at ARGS:wpTextbox1. [file "/usr/local/apache/conf/modsec2.user.conf"] [line "355"] [id "300016"] [rev "2"] [msg "Generic SQL injection protection"] [severity "CRITICAL"] [hostname "www.xsquawkbox.net"] [uri "/xpsdk/mediawiki/index.php"] [unique_id "TNra30PhuxAAAE8SUkMAAAAQ"]

Whoa. What is that? The server has ModSecurity installed, including a bunch of rules (as defined by regular expressions) designed to reject, um, bad stuff. The rule seems to come from here and MediaWiki isn't the only program that it can hose.

If you pull apart the regular expression, you can see how things go wrong. Loosely speaking the rule matches text in this form:

insert ___ into ___ values|select ___ from ___ from ___ insert|union ___ select|convert

where the blanks can be anything, can pipe indicates that either word is acceptable. So...insert, into, values, from, form, insert, convert. Those words appear in that sequence of comments in my OpenAL sample. And frankly, it's not a very remarkable sequence, hence it matching this.

So I thought the problem was long posts, but it wasn't. The longer the post, the more likely that a particular sequence of words would show up.

From what I can tell, white-listing URLs from the rule is the "standard" fix.

OpenAL on Three Platforms

OpenAL is a cross-platform 3-d sound API. It is not my favorite sound API, but it is cross-platform, which is pretty handy if you work on a cross-platform game. Keeping client code cross-platform with OpenAL is trivial (as long as you don't depend on particular vendor extensions) but actually getting an OpenAL runtime is a little bit trickier. This post describes a way to get OpenAL on three platforms without too much user hassle.

OS X

On OS X things are pretty easy: OpenAL ships with OS X as a framework dating back to, well, long enough that you don't have to worry about it. Link against the framework and go home happy.

Well, maybe you do have to worry. OpenAL started shipping with OS X with OS X 10.4. If you need to support 10.3.9, weak link against the framework and check an OpenAL symbol against null to handle a missing installation at run-time.

Linux

On Linux, OpenAL is typically in a shared object, e.g. libopenal.so. The problem is that the major version number of the .so changed from 0 to 1 when the reference implementation was replaced with OpenAL Soft. Since we were linking against libopenal.so.0, this broke X-Plane.

My first approach was to yell and complain in the general direction of the Linux community, but this didn't actually fix the problem. Instead, I wrote a wrapper around OpenAL, so that we could resolve function pointers from libraries opened with dlopen. Then I set X-Plane up to first try libopenal.so.1 and then libopenal.so.0.

(Why did the .so number change? The argument is that since the .0 version contained undocumented functions, technically the removal of those undocumented functions represents an ABI breakage. I don't quite buy this, as it punishes apps that follow the OpenAL spec to protect apps that didn't play by the rules. But again, my complaining has not changed the .so naming conventions.)

Windows

The Windows world is a bit more complicated because there are two separate things to consider:

• The implementation of OpenAL (e.g. who provided openal32.dll).
• The renderer (e.g. which code is actually producing audio).

Basically Creative Labs wanted to create an ecosystem like OpenGL where users would have drivers installed on their machine matching specialized hardware. So the Create implementation of openal32.dll searches for one or more renderers and can pass through OpenAL commands to any one of them. The standard OpenAL "redistributable" that Creative provides contains both this wrapper and a software-only renderer on top of DirectSound (the "generic software" renderer).

OpenAL Soft makes things interesting: you can install OpenAL soft into your system folder and it becomes yet another renderer. Or you can use it instead of any of the Creative components and then you get OpenAL soft and no possible extra renderers.

Now there's one other issue: what if there is no OpenAL runtime on the user's machine? DirectSound is pretty widely available, but OpenAL is not.

Here we take advantage of our DLL wrapper from the Linux case above: we package OpenAL Soft with the app as a DLL (it's LGPL). We first try to open openal32.dll in the system folder (the official way), but if that fails, we fall back and open our own copy of LibOpenAL Soft. Now we have sound everywhere and hardware acceleration if it's available.

One final note: in order to safely support third party windows renderers like Rapture3D, we need to give the user a way to pick among multiple devices, rather than always opening the default device (which is standard practice on Mac/Linux). This can be done with some settings UI or some heuristic to pick renderers.